Vertical Shift In An Equation
three.6: Transformation of Functions
- Page ID
- 15057
Learning Objectives
- Graph functions using vertical and horizontal shifts.
- Graph functions using reflections nearly the x-axis and the y-axis.
- Decide whether a function is even, odd, or neither from its graph.
- Graph functions using compressions and stretches.
- Combine transformations.
Nosotros all know that a flat mirror enables the states to come across an accurate image of ourselves and any is behind us. When nosotros tilt the mirror, the images we see may shift horizontally or vertically. But what happens when we bend a flexible mirror? Similar a funfair funhouse mirror, it presents us with a distorted paradigm of ourselves, stretched or compressed horizontally or vertically. In a similar mode, we can distort or transform mathematical functions to better accommodate them to describing objects or processes in the real world. In this department, we will take a look at several kinds of transformations.

Often when given a trouble, we try to model the scenario using mathematics in the form of words, tables, graphs, and equations. I method nosotros can utilize is to adapt the basic graphs of the toolkit functions to build new models for a given scenario. There are systematic ways to alter functions to construct appropriate models for the problems we are trying to solve.
Identifying Vertical Shifts
One elementary kind of transformation involves shifting the entire graph of a role upward, down, right, or left. The simplest shift is a vertical shift, moving the graph up or down, because this transformation involves adding a positive or negative constant to the function. In other words, we add the aforementioned constant to the output value of the function regardless of the input. For a office \(thousand(ten)=f(x)+chiliad\), the office \(f(ten)\) is shifted vertically \(1000\) units. Come across Figure \(\PageIndex{two}\) for an example.
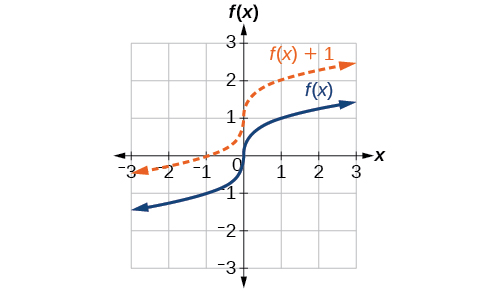
To assistance you visualize the concept of a vertical shift, consider that \(y=f(x)\). Therefore, \(f(x)+k\) is equivalent to \(y+k\). Every unit of \(y\) is replaced by \(y+k\), and then the \(y\)-value increases or decreases depending on the value of \(k\). The result is a shift upward or downward.
Definition: Vertical Shift
Given a function \(f(x)\), a new office \(thousand(x)=f(x)+k\), where \(chiliad\) is a constant, is a vertical shift of the function \(f(x)\). All the output values change by \(k\) units. If \(m\) is positive, the graph will shift upwardly. If \(k\) is negative, the graph will shift down.
Example \(\PageIndex{1}\): Calculation a Constant to a Function
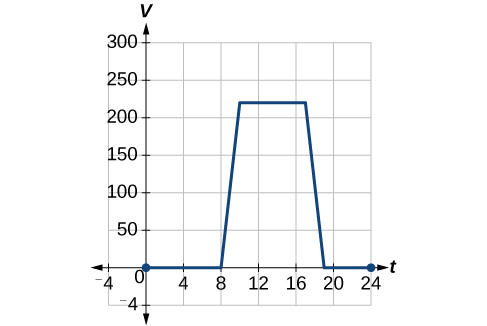
To regulate temperature in a green building, airflow vents almost the roof open and close throughout the day. Figure \(\PageIndex{iii}\) shows the area of open vents \(Five\) (in square feet) throughout the twenty-four hours in hours after midnight, \(t\). During the summer, the facilities manager decides to try to improve regulate temperature by increasing the corporeality of open vents past 20 foursquare feet throughout the twenty-four hours and night. Sketch a graph of this new function.
Solution
We can sketch a graph of this new function by calculation 20 to each of the output values of the original function. This will have the effect of shifting the graph vertically up, equally shown in Figure \(\PageIndex{4}\).
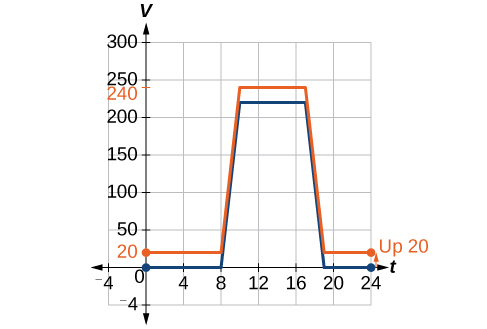
Discover that in Figure \(\PageIndex{iv}\), for each input value, the output value has increased by twenty, so if we phone call the new function \(S(t)\),we could write
\[S(t)=5(t)+twenty\]
This note tells us that, for any value of \(t\),\(S(t)\) can be found past evaluating the function \(V\) at the same input and and then adding xx to the result. This defines \(S\) as a transformation of the part \(V\), in this case a vertical shift upwards xx units. Notice that, with a vertical shift, the input values stay the aforementioned and only the output values alter. Come across Table \(\PageIndex{1}\).
| \(t\) | 0 | eight | 10 | 17 | xix | 24 |
|---|---|---|---|---|---|---|
| \(V(t)\) | 0 | 0 | 220 | 220 | 0 | 0 |
| \(S(t)\) | twenty | twenty | 240 | 240 | 20 | 20 |
How To...
Given a tabular function, create a new row to represent a vertical shift.
- Identify the output row or column.
- Determine the magnitude of the shift.
- Add the shift to the value in each output cell. Add a positive value for up or a negative value for down.
Example \(\PageIndex{2}\): Shifting a Tabular Part Vertically
A office \(f(10)\) is given in Table \(\PageIndex{2}\). Create a table for the function \(one thousand(ten)=f(x)−3\).
| \(ten\) | 2 | 4 | six | viii |
|---|---|---|---|---|
| \(f(x)\) | i | 3 | 7 | xi |
Solution
The formula \(g(x)=f(ten)−3\) tells u.s. that we tin find the output values of \(g\) past subtracting 3 from the output values of \(f\). For example:
\[\begin{marshal*} f(x)&=i &\text{Given} \\[4pt] thou(x)&=f(10)-3 &\text{Given Transformation} \\[4pt] g(2) & =f(2)−3 \\ &=1-3\\ &=-2\cease{align*}\]
Subtracting three from each \(f(x)\) value, we can complete a table of values for \(grand(10)\) equally shown in Table \(\PageIndex{3}\).
| \(x\) | 2 | 4 | six | 8 |
|---|---|---|---|---|
| \(f(x)\) | ane | three | 7 | eleven |
| \(g(x)\) | -2 | 0 | 4 | viii |
Analysis
As with the earlier vertical shift, notice the input values stay the aforementioned and merely the output values change.
Exercise \(\PageIndex{i}\)
The role \(h(t)=−4.9t^2+30t\) gives the height \(h\) of a ball (in meters) thrown upward from the footing afterward \(t\) seconds. Suppose the brawl was instead thrown from the top of a ten-m edifice. Relate this new pinnacle function \(b(t)\) to \(h(t)\), and so find a formula for \(b(t)\).
- Answer
-
\(b(t)=h(t)+10=−4.9t^two+30t+10\)
Identifying Horizontal Shifts
Nosotros just saw that the vertical shift is a change to the output, or outside, of the function. Nosotros will now look at how changes to input, on the inside of the part, change its graph and meaning. A shift to the input results in a movement of the graph of the function left or right in what is known equally a horizontal shift, shown in Figure \(\PageIndex{four}\).
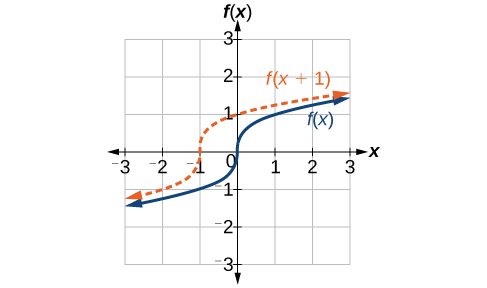
For example, if \(f(x)=x^2\), then \(thou(ten)=(x−2)^2\) is a new function. Each input is reduced by ii prior to squaring the function. The upshot is that the graph is shifted 2 units to the right, because we would demand to increment the prior input past ii units to yield the aforementioned output value as given in \(f\).
Definition: Horizontal Shift
Given a function \(f\), a new part \(thousand(x)=f(10−h)\), where \(h\) is a constant, is a horizontal shift of the function \(f\). If \(h\) is positive, the graph will shift correct. If \(h\) is negative, the graph will shift left.
Case \(\PageIndex{iv}\): Adding a Constant to an Input
Returning to our building airflow example from Figure \(\PageIndex{2}\), suppose that in fall the facilities manager decides that the original venting plan starts too late, and wants to begin the entire venting plan 2 hours earlier. Sketch a graph of the new office.
Solution
Nosotros tin can set \(V(t)\) to be the original plan and \(F(t)\) to be the revised program.
\[V(t)= \text{ the original venting plan} \nonumber\]
\[F(t)= \text{ starting 2 hrs sooner} \nonumber\]
In the new graph, at each time, the airflow is the same every bit the original role \(Five\) was 2 hours later. For case, in the original part \(V\), the airflow starts to change at 8 a.one thousand., whereas for the function \(F\), the airflow starts to change at 6 a.k. The comparable function values are \(V(8)=F(6)\). See Figure \(\PageIndex{five}\). Notice also that the vents get-go opened to \(220 \text{ft}^2\) at 10 a.one thousand. under the original programme, while under the new program the vents reach \(220 \text{ft}^2\) at 8 a.g., so \(V(10)=F(8)\).
In both cases, nosotros run across that, because \(F(t)\) starts two hours sooner, \(h=−2\). That means that the same output values are reached when \(F(t)=V(t−(−two))=5(t+2)\).
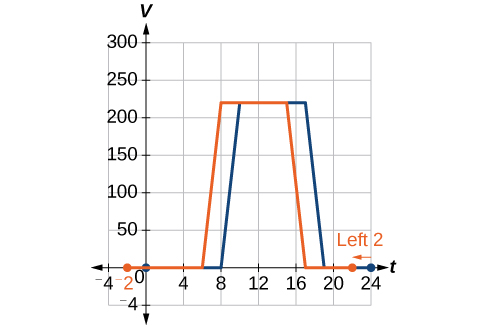
Assay
Note that \(V(t+2)\) has the effect of shifting the graph to the left.
Horizontal changes or "within changes" affect the domain of a function (the input) instead of the range and ofttimes seem counterintuitive. The new function \(F(t)\) uses the same outputs as \(V(t)\), but matches those outputs to inputs 2 hours earlier than those of \(V(t)\). Said another mode, we must add ii hours to the input of \(V\) to find the corresponding output for \(F:F(t)=V(t+ii)\).
How To...
Given a tabular role, create a new row to represent a horizontal shift.
- Identify the input row or cavalcade.
- Determine the magnitude of the shift.
- Add the shift to the value in each input jail cell.
Example \(\PageIndex{5}\): Shifting a Tabular Part Horizontally
A function \(f(10)\) is given in Table \(\PageIndex{4}\). Create a table for the function \(thou(ten)=f(x−3)\).
| \(ten\) | 2 | iv | vi | 8 |
|---|---|---|---|---|
| \(f(x)\) | 1 | iii | vii | eleven |
Solution
The formula \(g(x)=f(x−iii)\) tells usa that the output values of \(1000\) are the same as the output value of \(f\) when the input value is 3 less than the original value. For example, we know that \(f(ii)=one\). To become the aforementioned output from the function \(g\), we will need an input value that is 3 larger. We input a value that is 3 larger for \(thousand(10)\) because the function takes iii abroad before evaluating the function \(f\).
\[\brainstorm{align*} g(5)&=f(5-3) \\ &=f(2) \\ &=i \finish{align*}\]
We keep with the other values to create Table \(\PageIndex{5}\).
| \(x\) | v | vii | 9 | 11 |
|---|---|---|---|---|
| \(x-3\) | 2 | 4 | six | eight |
| \(f(x)\) | i | 3 | seven | eleven |
| \(g(10)\) | one | 3 | 7 | 11 |
The result is that the part \(yard(x)\) has been shifted to the right by iii. Detect the output values for \(1000(ten)\) remain the aforementioned as the output values for \(f(x)\), merely the corresponding input values, \(x\), have shifted to the right by 3. Specifically, two shifted to 5, 4 shifted to 7, 6 shifted to 9, and 8 shifted to 11.
Assay
Figure \(\PageIndex{six}\) represents both of the functions. We can see the horizontal shift in each point.
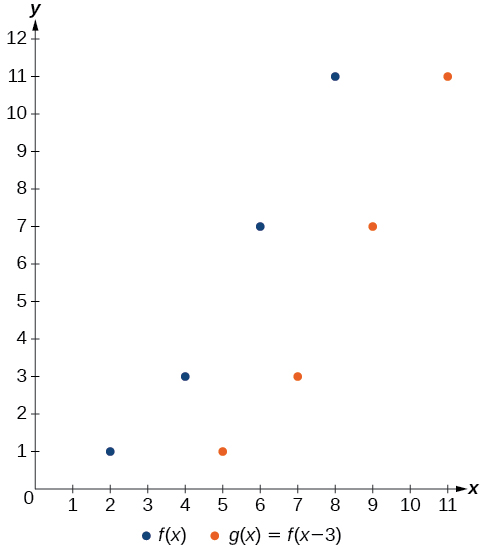
Example \(\PageIndex{6}\): Identifying a Horizontal Shift of a Toolkit Role
Effigy \(\PageIndex{7}\) represents a transformation of the toolkit function \(f(x)=x^2\). Relate this new part \(g(x)\) to \(f(10)\), and then discover a formula for \(g(x)\).
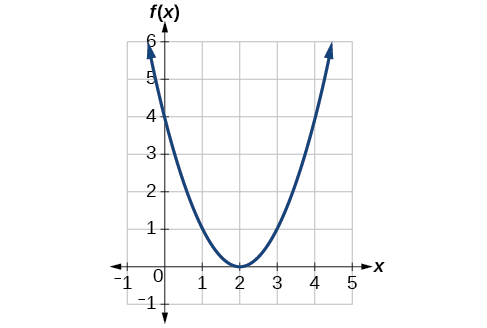
Solution
Notice that the graph is identical in shape to the \(f(10)=10^two\) function, merely the \(x\)-values are shifted to the right 2 units. The vertex used to be at \((0,0)\), but now the vertex is at \((2,0)\). The graph is the basic quadratic function shifted two units to the correct, so
\[k(x)=f(x−2) \nonumber\]
Observe how we must input the value \(x=2\) to get the output value \(y=0\); the \(x\)-values must be 2 units larger considering of the shift to the correct by 2 units. We tin can then use the definition of the \(f(x)\) function to write a formula for \(g(x)\) by evaluating \(f(x−ii)\).
\[\brainstorm{align*} f(x)&=x^ii \\ g(x)&=f(ten-2) \\ g(x)&=f(x-two)=(x-ii)^ii \end{align*}\]
Analysis
To determine whether the shift is \(+two\) or \(−2\), consider a single reference signal on the graph. For a quadratic, looking at the vertex betoken is convenient. In the original office, \(f(0)=0\). In our shifted office, \(g(2)=0\). To obtain the output value of 0 from the function \(f\), we need to decide whether a plus or a minus sign will piece of work to satisfy \(g(2)=f(x−2)=f(0)=0\). For this to piece of work, we will need to subtract 2 units from our input values.
Example \(\PageIndex{vii}\): Interpreting Horizontal versus Vertical Shifts
The function \(G(grand)\) gives the number of gallons of gas required to bulldoze \(1000\) miles. Interpret \(Thou(m)+10\) and \(1000(m+10)\)
Solution
\(G(1000)+x\) can be interpreted as adding 10 to the output, gallons. This is the gas required to drive \(k\) miles, plus another ten gallons of gas. The graph would bespeak a vertical shift.
\(G(m+10)\) can be interpreted every bit adding ten to the input, miles. So this is the number of gallons of gas required to drive 10 miles more than \(grand\) miles. The graph would betoken a horizontal shift.
Do \(\PageIndex{seven}\)
Given the function \(f(ten)=\sqrt{x}\), graph the original function \(f(x)\) and the transformation \(1000(x)=f(x+2)\) on the aforementioned axes. Is this a horizontal or a vertical shift? Which way is the graph shifted and by how many units?
- Answer
-
The graphs of \(f(x)\) and \(yard(x)\) are shown beneath. The transformation is a horizontal shift. The function is shifted to the left past 2 units.
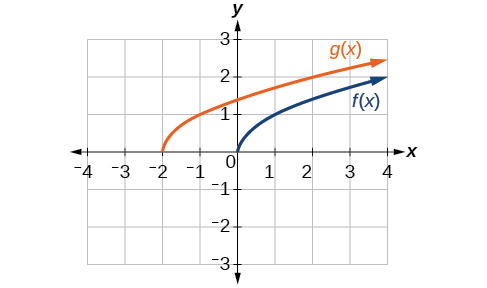
Figure \(\PageIndex{8}\)
Combining Vertical and Horizontal Shifts
Now that we have two transformations, we tin can combine them together. Vertical shifts are outside changes that affect the output \((y-)\) centrality values and shift the part up or down. Horizontal shifts are inside changes that affect the input \((x-)\) axis values and shift the function left or right. Combining the two types of shifts will cause the graph of a function to shift up or down and right or left.
How To...
Given a function and both a vertical and a horizontal shift, sketch the graph.
- Identify the vertical and horizontal shifts from the formula.
- The vertical shift results from a constant added to the output. Movement the graph up for a positive constant and down for a negative abiding.
- The horizontal shift results from a abiding added to the input. Move the graph left for a positive constant and right for a negative constant.
- Utilise the shifts to the graph in either guild.
Example \(\PageIndex{8}\): Graphing Combined Vertical and Horizontal Shifts
Given \(f(x)=|10|\), sketch a graph of \(h(10)=f(ten+1)−3\).
Solution
The office \(f\) is our toolkit absolute value function. We know that this graph has a V shape, with the point at the origin. The graph of \(h\) has transformed \(f\) in two means: \(f(x+one)\) is a change on the inside of the function, giving a horizontal shift left past 1, and the subtraction by 3 in \(f(x+1)−3\) is a modify to the outside of the role, giving a vertical shift down past 3. The transformation of the graph is illustrated in Figure \(\PageIndex{9}\).
Let united states follow one betoken of the graph of \(f(x)=|x|\).
- The betoken \((0,0)\) is transformed first by shifting left 1 unit:\((0,0)\rightarrow(−1,0)\)
- The point \((−1,0)\) is transformed side by side by shifting down 3 units:\((−1,0)\rightarrow(−1,−iii)\)
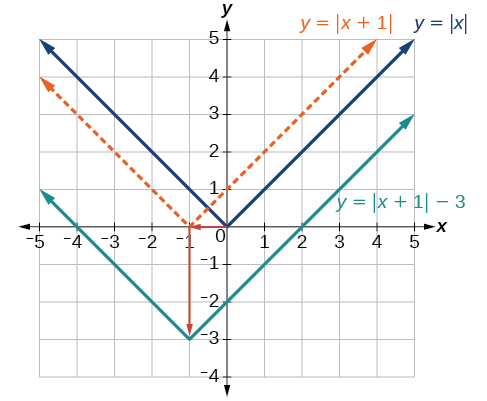
Figure \(\PageIndex{10}\) shows the graph of \(h\).
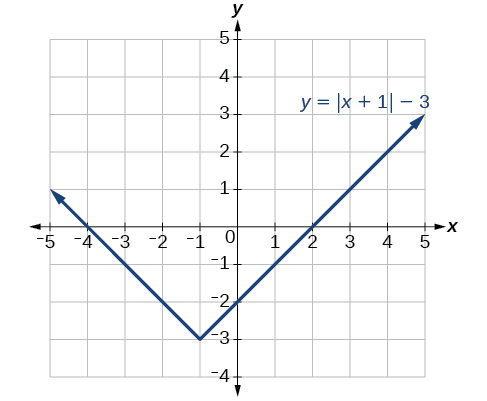
Exercise \(\PageIndex{viii}\)
Given \(f(x)=|x|\), sketch a graph of \(h(x)=f(10−2)+4\).
- Answer
-
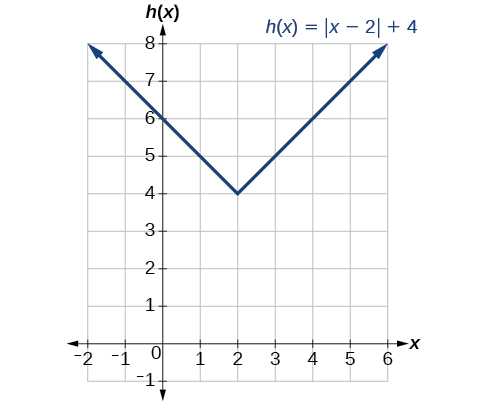
Figure \(\PageIndex{11}\)
Example \(\PageIndex{9}\): Identifying Combined Vertical and Horizontal Shifts
Write a formula for the graph shown in Figure \(\PageIndex{12}\), which is a transformation of the toolkit foursquare root function.
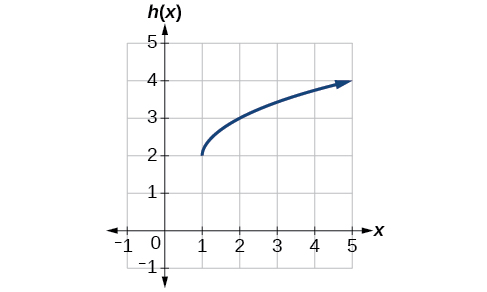
Solution
The graph of the toolkit role starts at the origin, and so this graph has been shifted 1 to the right and up 2. In office notation, we could write that every bit
\[h(10)=f(x−ane)+ii \nonumber\]
Using the formula for the square root function, we can write
\[h(x)=\sqrt{x−one}+2 \nonumber\]
Analysis
Annotation that this transformation has changed the domain and range of the part. This new graph has domain \(\left[1,\infty\right)\) and range \(\left[two,\infty\right)\).
Exercise \(\PageIndex{ix}\)
Write a formula for a transformation of the toolkit reciprocal role \(f(x)=\frac{i}{ten}\) that shifts the function'southward graph ane unit to the right and one unit up.
- Answer
-
\[g(ten)=\dfrac{1}{x-one}+i \nonumber \]
Graphing Functions Using Reflections about the Axes
Another transformation that can be practical to a role is a reflection over the x- or y-centrality. A vertical reflection reflects a graph vertically across the 10-axis, while a horizontal reflection reflects a graph horizontally across the y-centrality. The reflections are shown in Figure \(\PageIndex{13}\).
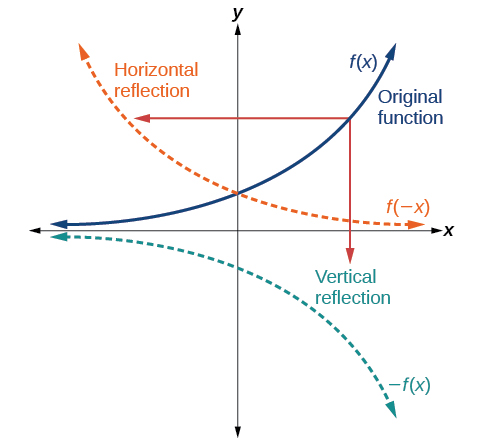 .
. Notice that the vertical reflection produces a new graph that is a mirror image of the base of operations or original graph most the ten-axis. The horizontal reflection produces a new graph that is a mirror image of the base or original graph about the y-axis.
Definitions: Reflections
Given a function \(f(x)\), a new function \(chiliad(x)=−f(x)\) is a vertical reflection of the part \(f(10)\), sometimes called a reflection almost (or over, or through) the x-axis.
Given a office \(f(10)\), a new office \(g(x)=f(−10)\) is a horizontal reflection of the office \(f(10)\), sometimes called a reflection about the y-axis.
How To...
Given a office, reflect the graph both vertically and horizontally.
- Multiply all outputs by –one for a vertical reflection. The new graph is a reflection of the original graph about the 10-axis.
- Multiply all inputs by –ane for a horizontal reflection. The new graph is a reflection of the original graph about the y-centrality.
Example \(\PageIndex{10}\): Reflecting a Graph Horizontally and Vertically
Reverberate the graph of \(s(t)=\sqrt{t}\) (a) vertically and (b) horizontally.
Solution
a. Reflecting the graph vertically ways that each output value will be reflected over the horizontal t-centrality equally shown in Figure \(\PageIndex{xiv}\).
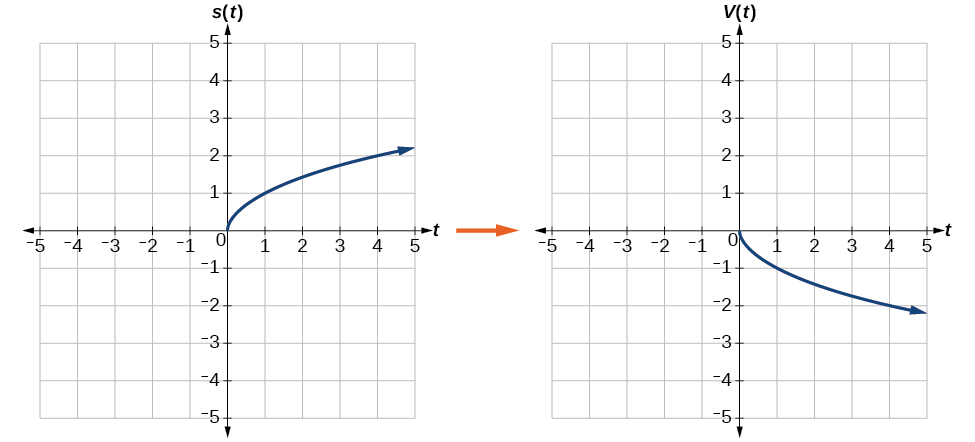
Because each output value is the reverse of the original output value, we tin can write
\[V(t)=−due south(t) \text{ or } V(t)=−\sqrt{t} \nonumber\]
Notice that this is an exterior alter, or vertical shift, that affects the output \(s(t)\) values, so the negative sign belongs outside of the office.
b. Reflecting horizontally means that each input value will be reflected over the vertical axis as shown in Figure \(\PageIndex{15}\).
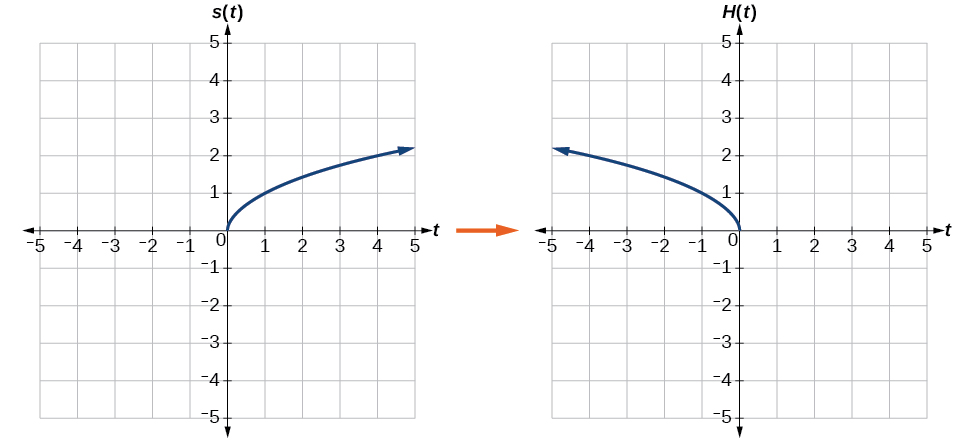
Because each input value is the opposite of the original input value, we can write
\[H(t)=s(−t) \text{ or } H(t)=\sqrt{−t} \nonumber\]
Notice that this is an inside alter or horizontal alter that affects the input values, so the negative sign is on the inside of the function.
Note that these transformations can impact the domain and range of the functions. While the original square root role has domain \(\left[0,\infty\right)\) and range \(\left[0,\infty\right)\), the vertical reflection gives the \(Five(t)\) role the range \(\left(−\infty,0\right]\) and the horizontal reflection gives the \(H(t)\) office the domain \(\left(−\infty, 0\right]\).
Exercise \(\PageIndex{5}\)
Reflect the graph of \(f(10)=|x−1|\) (a) vertically and (b) horizontally.
- Answer
-
a.
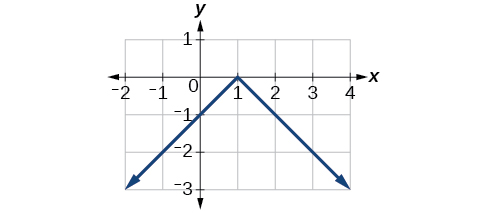
Figure \(\PageIndex{xvi}\): Graph of a vertically reflected absolute role. b.
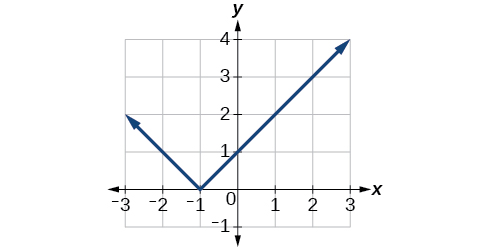
Figure \(\PageIndex{17}\): Graph of an accented function translated i unit left.
Instance \(\PageIndex{11}\): Reflecting a Tabular Function Horizontally and Vertically
A function \(f(x)\) is given as Table \(\PageIndex{6}\). Create a tabular array for the functions below.
a. \(k(x)=−f(x)\)
b. \(h(ten)=f(−x)\)
| \(ten\) | two | iv | 6 | eight |
|---|---|---|---|---|
| \(f(x)\) | 1 | 3 | 7 | 11 |
a. For \(g(x)\), the negative sign outside the office indicates a vertical reflection, so the ten-values stay the same and each output value will be the opposite of the original output value. See Table \(\PageIndex{7}\).
| \(10\) | two | 4 | 6 | 8 |
|---|---|---|---|---|
| \(g(x)\) | -ane | -iii | -7 | -eleven |
b. For \(h(x)\), the negative sign inside the office indicates a horizontal reflection, so each input value volition exist the reverse of the original input value and the \(h(ten)\) values stay the same as the \(f(x)\) values. See Table \(\PageIndex{8}\).
| \(ten\) | -2 | -4 | -6 | -eight |
|---|---|---|---|---|
| \(h(x)\) | 1 | 3 | 7 | 11 |
Exercise \(\PageIndex{6}\)
A part \(f(x)\) is given as Table \(\PageIndex{ix}\). Create a table for the functions below.
a. \(g(x)=−f(x)\)
b. \(h(x)=f(−x)\)
| \(x\) | -2 | 0 | 2 | 4 |
|---|---|---|---|---|
| \(f(x)\) | 5 | 10 | 15 | 20 |
- Reply
-
a. \(g(x)=−f(x)\)
Table \(\PageIndex{10}\) \(x\) -2 0 ii 4 \(g(x)\) -5 -x -15 -20 b. \(h(x)=f(−x)\)
Table \(\PageIndex{11}\) \(x\) -two 0 2 -4 \(h(ten)\) fifteen 10 5 20
Example \(\PageIndex{12}\): Applying a Learning Model Equation
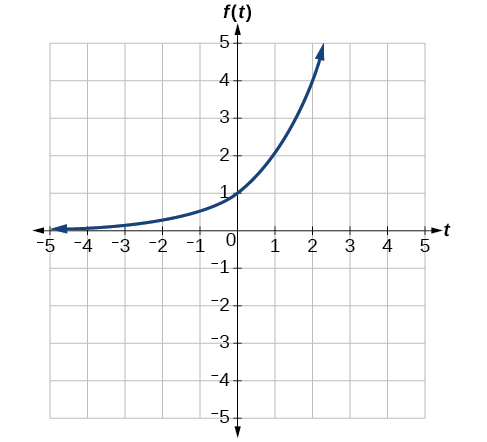
A common model for learning has an equation similar to \(k(t)=−2^{−t}+1\), where \(one thousand\) is the pct of mastery that tin be achieved after \(t\) practice sessions. This is a transformation of the part \(f(t)=ii^t\) shown in Figure \(\PageIndex{xviii}\). Sketch a graph of \(m(t)\).
Solution
This equation combines three transformations into one equation.
- A horizontal reflection: \(f(−t)=2^{−t}\)
- A vertical reflection: \(−f(−t)=−two^{−t}\)
- A vertical shift: \(−f(−t)+1=−2^{−t}+1\)
We can sketch a graph past applying these transformations one at a time to the original function. Let u.s. follow two points through each of the three transformations. We volition choose the points \((0, one)\) and \((1, 2)\).
- First, nosotros apply a horizontal reflection: \((0, one) \; (–1, ii)\).
- Then, we utilize a vertical reflection: \((0, −i) \; (-one, –2)\).
- Finally, we apply a vertical shift: \((0, 0) \; (-ane, -i)\).
This means that the original points, \((0,1)\) and \((1,two)\) become \((0,0)\) and \((-1,-1)\) after nosotros utilize the transformations.
In Figure \(\PageIndex{19}\), the start graph results from a horizontal reflection. The 2nd results from a vertical reflection. The third results from a vertical shift up ane unit.
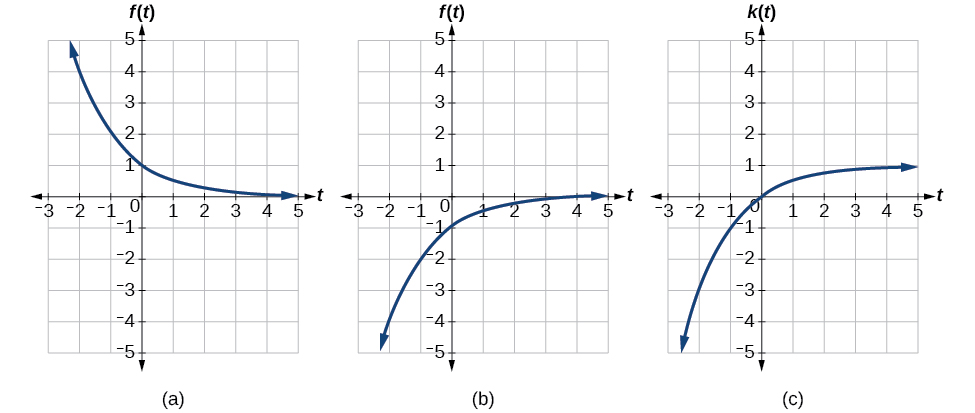
Assay
As a model for learning, this office would exist limited to a domain of \(t\geq0\), with corresponding range \(\left[0,1\correct)\).
Exercise \(\PageIndex{7}\)
Given the toolkit function \(f(10)=x^2\), graph \(g(x)=−f(x)\) and \(h(x)=f(−10)\). Take note of any surprising beliefs for these functions.
- Answer
-
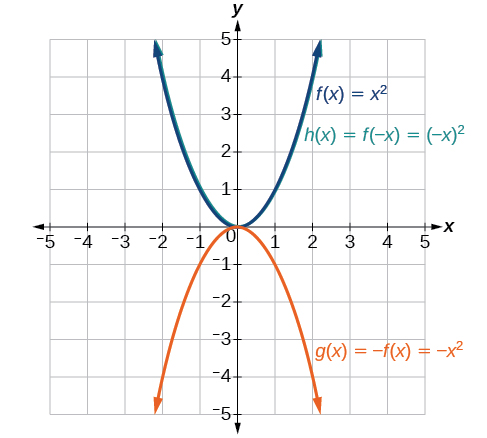
Figure \(\PageIndex{20}\): Graph of \(ten^two\) and its reflections. Observe: \(g(10)=f(−x)\) looks the same as \(f(ten)\).
Determining Even and Odd Functions
Some functions showroom symmetry so that reflections effect in the original graph. For instance, horizontally reflecting the toolkit functions \(f(ten)=x^2\) or \(f(10)=|ten|\) will result in the original graph. We say that these types of graphs are symmetric about the y-axis. Functions whose graphs are symmetric about the y-axis are called even functions.
If the graphs of \(f(x)=ten^three\) or \(f(x)=\frac{1}{x}\) were reflected over both axes, the effect would be the original graph, every bit shown in Figure \(\PageIndex{21}\).
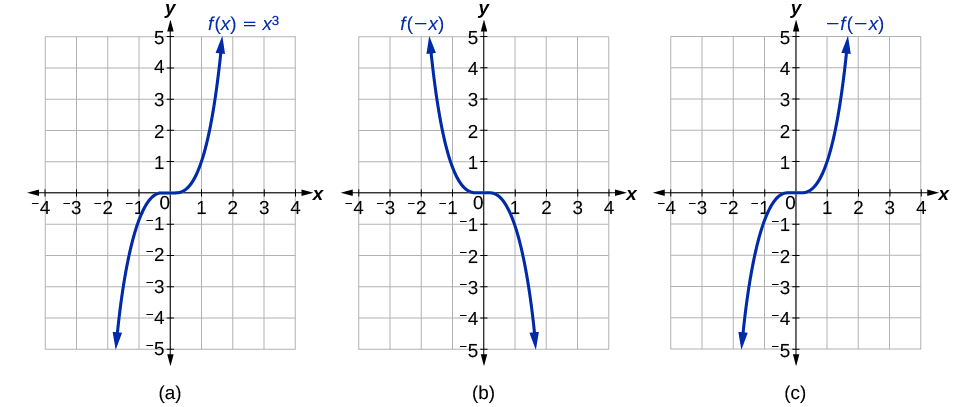
We say that these graphs are symmetric about the origin. A function with a graph that is symmetric near the origin is chosen an odd function.
Notation: A function can be neither even nor odd if it does not exhibit either symmetry. For case, \(f(x)=two^x\) is neither even nor odd. Also, the only part that is both even and odd is the abiding office \(f(10)=0\).
Definitions: Even and Odd Functions
A function is called an even function if for every input \(10\)
\(f(x)=f(−x)\)
The graph of an even part is symmetric nigh the y-axis.
A role is chosen an odd function if for every input \(x\)
\(f(10)=−f(−x)\)
The graph of an odd function is symmetric about the origin.
How To...
Given the formula for a function, determine if the function is fifty-fifty, odd, or neither.
- Determine whether the function satisfies \(f(x)=f(−ten)\). If it does, it is fifty-fifty.
- Determine whether the part satisfies \(f(10)=−f(−x)\). If information technology does, it is odd.
- If the office does non satisfy either rule, it is neither even nor odd.
Instance \(\PageIndex{13}\): Determining whether a Role Is Even, Odd, or Neither
Is the role \(f(x)=x^3+2x\) even, odd, or neither?
Solution
Without looking at a graph, we can decide whether the function is even or odd past finding formulas for the reflections and determining if they return us to the original function. Permit's begin with the dominion for even functions.
\[f(−x)=(−x)^3+ii(−ten)=−x^3−2x \nonumber\]
This does not return us to the original office, and so this function is not even. Nosotros can now examination the rule for odd functions.
\[−f(−x)=−(−x^3−2x)=x^iii+2x \nonumber\]
Because \(−f(−x)=f(x)\), this is an odd function.
Analysis
Consider the graph of \(f\) in Figure \(\PageIndex{22}\). Notice that the graph is symmetric about the origin. For every bespeak \((ten,y)\) on the graph, the corresponding point \((−x,−y)\) is besides on the graph. For example, \((1, 3)\) is on the graph of \(f\), and the corresponding point \((−one,−3)\) is too on the graph.

Exercise \(\PageIndex{viii}\)
Is the part \(f(south)=s^4+3s^2+seven\) even, odd, or neither?
- Answer
-
fifty-fifty
Graphing Functions Using Stretches and Compressions
Adding a constant to the inputs or outputs of a function changed the position of a graph with respect to the axes, only information technology did non bear on the shape of a graph. We now explore the effects of multiplying the inputs or outputs by some quantity.
We can transform the inside (input values) of a function or nosotros can transform the exterior (output values) of a function. Each change has a specific effect that can be seen graphically.
Vertical Stretches and Compressions
When we multiply a function by a positive abiding, we get a function whose graph is stretched or compressed vertically in relation to the graph of the original function. If the abiding is greater than ane, we get a vertical stretch; if the abiding is between 0 and i, nosotros get a vertical compression. Figure \(\PageIndex{23}\) shows a function multiplied by constant factors ii and 0.five and the resulting vertical stretch and compression.
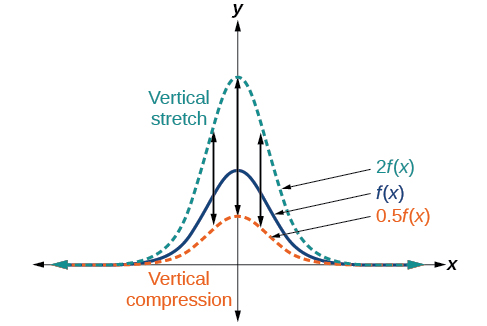
Definitions: Vertical Stretches and Compressions
Given a function \(f(x)\), a new function \(g(10)=af(x)\), where \(a\) is a abiding, is a vertical stretch or vertical compression of the part \(f(x)\).
- If \(a>ane\), and then the graph volition be stretched.
- If \(0<a<1\), then the graph will be compressed.
- If \(a<0\), and then in that location will exist combination of a vertical stretch or compression with a vertical reflection.
How To...
Given a function, graph its vertical stretch.
- Identify the value of \(a\).
- Multiply all range values by \(a\)
- If \(a>ane\), the graph is stretched by a factor of \(a\).
- If \(0<a<1\), the graph is compressed past a factor of \(a\).
- If \(a<0\), the graph is either stretched or compressed and too reflected about the x-axis.
Example 1.five.14: Graphing a Vertical Stretch
A function \(P(t)\) models the population of fruit flies. The graph is shown in Effigy \(\PageIndex{24}\).
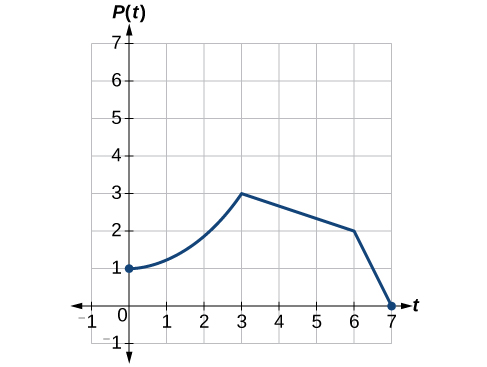
A scientist is comparing this population to another population, \(Q\), whose growth follows the same pattern, merely is twice as large. Sketch a graph of this population.
Solution
Because the population is always twice as big, the new population's output values are e'er twice the original function's output values. Graphically, this is shown in Effigy \(\PageIndex{25}\).
If nosotros choose 4 reference points, \((0, 1)\), \((iii, 3)\), \((half dozen, 2)\) and \((7, 0)\) nosotros volition multiply all of the outputs past 2.
The following shows where the new points for the new graph will be located.
\[(0, one)\rightarrow(0, 2)\]
\[(3, 3)\rightarrow(3, 6)\]
\[(half-dozen, two)\rightarrow(six, 4)\]
\[(vii, 0)\rightarrow(vii, 0)\]
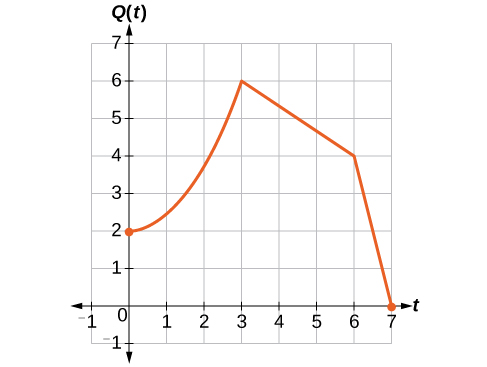
Symbolically, the relationship is written equally
\[Q(t)=2P(t) \nonumber\]
This means that for any input \(t\), the value of the part \(Q\) is twice the value of the office \(P\). Notice that the upshot on the graph is a vertical stretching of the graph, where every point doubles its distance from the horizontal axis. The input values, \(t\), stay the aforementioned while the output values are twice every bit large equally before.
How To...
Given a tabular function and assuming that the transformation is a vertical stretch or compression, create a table for a vertical pinch.
- Make up one's mind the value of \(a\).
- Multiply all of the output values by \(a\).
Example \(\PageIndex{15}\): Finding a Vertical Compression of a Tabular Part
A office \(f\) is given as Table \(\PageIndex{12}\). Create a tabular array for the part \(1000(ten)=\frac{1}{2}f(x)\).
| \(x\) | two | 4 | vi | viii |
|---|---|---|---|---|
| \(f(x)\) | 1 | 3 | 7 | eleven |
Solution
The formula \(g(x)=\frac{1}{2}f(ten)\) tells us that the output values of \(chiliad\) are half of the output values of \(f\) with the same inputs. For example, nosotros know that \(f(iv)=3\). And so
\[g(4)=\frac{1}{two}f(iv)=\frac{1}{2}(3)=\frac{3}{ii} \nonumber\]
We do the same for the other values to produce Table \(\PageIndex{13}\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(g(x)\) | \(\dfrac{ane}{2}\) | \(\dfrac{3}{2}\) | \(\dfrac{vii}{2}\) | \(\dfrac{11}{ii}\) |
Analysis
The upshot is that the role \(g(ten)\) has been compressed vertically by \(\frac{i}{two}\). Each output value is divided in half, so the graph is one-half the original height.
Exercise \(\PageIndex{9}\)
A role \(f\) is given equally Table \(\PageIndex{14}\). Create a table for the role \(g(x)=\frac{three}{4}f(x)\).
| \(x\) | 2 | 4 | 6 | eight |
|---|---|---|---|---|
| \(f(10)\) | 12 | 16 | 20 | 0 |
- Answer
-
Table \(\PageIndex{xv}\) \(x\) 2 four 6 8 \(g(x)\) 9 12 fifteen 0
Example \(\PageIndex{16}\): Recognizing a Vertical Stretch
The graph in Figure \(\PageIndex{26}\) is a transformation of the toolkit part \(f(x)=x^3\). Relate this new function \(k(x)\) to \(f(ten)\), and then find a formula for \(g(x)\).
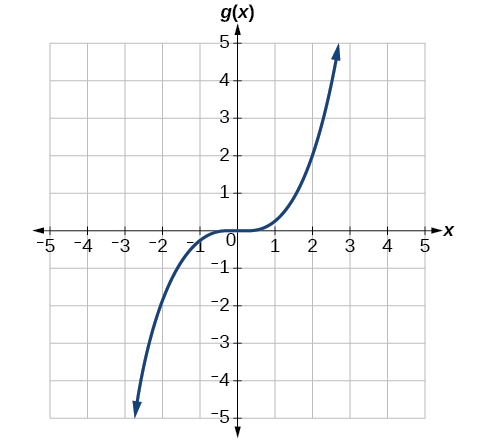
When trying to determine a vertical stretch or shift, information technology is helpful to look for a point on the graph that is relatively articulate. In this graph, it appears that \(chiliad(ii)=2\). With the basic cubic function at the aforementioned input, \(f(two)=2^three=8\). Based on that, it appears that the outputs of \(g\) are \(\frac{i}{4}\) the outputs of the office \(f\) because \(g(2)=\frac{1}{4}f(ii)\). From this we can fairly safely conclude that \(g(x)=\frac{one}{iv}f(x)\).
Nosotros tin can write a formula for \(g\) by using the definition of the part \(f\).
\[g(x)=\frac{1}{4} f(x)=\frac{1}{4}10^three.\]
Exercise \(\PageIndex{1}\)
Write the formula for the function that nosotros get when we stretch the identity toolkit office past a factor of three, then shift it downwardly by 2 units.
- Reply
-
\(g(x)=3x-2\)
Horizontal Stretches and Compressions
Now we consider changes to the within of a role. When we multiply a function'south input by a positive constant, we get a function whose graph is stretched or compressed horizontally in relation to the graph of the original role. If the abiding is betwixt 0 and 1, we get a horizontal stretch; if the constant is greater than 1, we get a horizontal compression of the role.
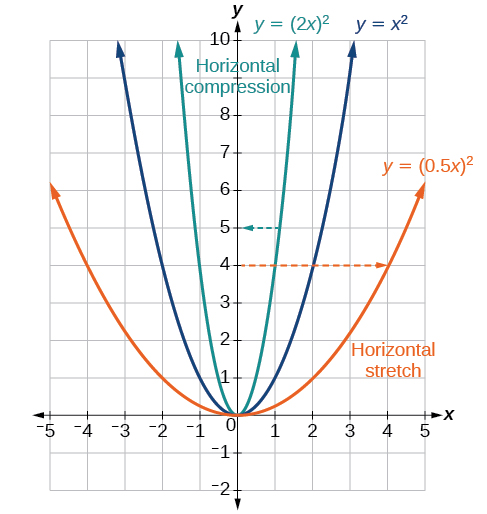
Given a function \(y=f(x)\), the form \(y=f(bx)\) results in a horizontal stretch or compression. Consider the office \(y=x^ii\). Detect Figure \(\PageIndex{27}\). The graph of \(y=(0.5x)^two\) is a horizontal stretch of the graph of the function \(y=x^2\) by a gene of 2. The graph of \(y=(2x)^two\) is a horizontal compression of the graph of the part \(y=x^2\) by a cistron of 2.
Definitions: Horizontal Stretches and Compressions
Given a function \(f(x)\), a new function \(g(10)=f(bx)\), where \(b\) is a constant, is a horizontal stretch or horizontal pinch of the office \(f(ten)\).
- If \(b>1\), and then the graph will exist compressed by \(\frac{1}{b}\).
- If \(0<b<one\), then the graph will be stretched past \(\frac{1}{b}\).
- If \(b<0\), then there volition be combination of a horizontal stretch or compression with a horizontal reflection.
How To...
Given a description of a part, sketch a horizontal compression or stretch.
- Write a formula to represent the function.
- Set up \(thousand(x)=f(bx)\) where \(b>1\) for a compression or \(0<b<1\) for a stretch.
Example \(\PageIndex{17}\): Graphing a Horizontal Compression
Suppose a scientist is comparing a population of fruit flies to a population that progresses through its lifespan twice equally fast as the original population. In other words, this new population, \(R\), will progress in 1 60 minutes the same amount as the original population does in ii hours, and in 2 hours, it will progress as much as the original population does in 4 hours. Sketch a graph of this population.
Solution
Symbolically, nosotros could write
\(\brainstorm{align} R(one)&=P(2), \\ R(two)&=P(iv), &\text{and in full general,} \\ R(t)&=P(2t).\end{align}\)
See Effigy \(\PageIndex{28}\) for a graphical comparison of the original population and the compressed population.
![Two side-by-side graphs. The first graph has function for original population whose domain is [0,7] and range is [0,3]. The maximum value occurs at (3,3). The second graph has the same shape as the first except it is half as wide. It is a graph of transformed population, with a domain of [0, 3.5] and a range of [0,3]. The maximum occurs at (1.5, 3).](https://math.libretexts.org/@api/deki/files/995/CNX_Precalc_Figure_01_05_029ab.jpg?revision=1)
Analysis
Note that the effect on the graph is a horizontal compression where all input values are one-half of their original distance from the vertical axis.
Case \(\PageIndex{18}\): Finding a Horizontal Stretch for a Tabular Part
A function \(f(x)\) is given as Table \(\PageIndex{16}\). Create a table for the part \(g(x)=f(\frac{1}{ii}x)\).
| \(x\) | 2 | 4 | 6 | 8 |
|---|---|---|---|---|
| \(f(x)\) | ane | 3 | seven | 11 |
The formula \(yard(x)=f(\frac{1}{2}x)\) tells us that the output values for \(g\) are the same as the output values for the office \(f\) at an input half the size. Notice that nosotros do not take enough information to make up one's mind \(g(2)\) because \(one thousand(2)=f(\frac{1}{2}⋅two)=f(i)\), and we practise not take a value for \(f(1)\) in our table. Our input values to \(g\) will need to exist twice as large to get inputs for \(f\) that we can evaluate. For example, we can make up one's mind \(g(four)\).
\[g(4)=f(\dfrac{1}{2}⋅4)=f(two)=ane\]
We practise the same for the other values to produce Table \(\PageIndex{17}\).
| \(x\) | 4 | 8 | 12 | 16 |
|---|---|---|---|---|
| \(g(10)\) | 1 | 3 | vii | eleven |
Figure \(\PageIndex{29}\) shows the graphs of both of these sets of points.
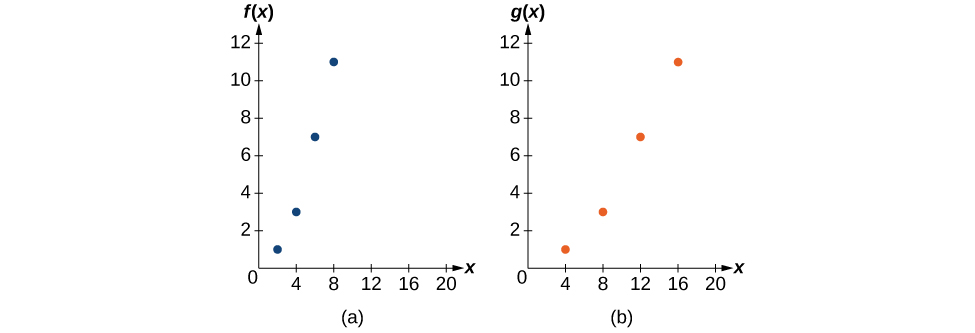
Analysis
Because each input value has been doubled, the result is that the function \(g(x)\) has been stretched horizontally by a factor of 2.
Example \(\PageIndex{nineteen}\): Recognizing a Horizontal Compression on a Graph
Relate the function \(one thousand(x)\) to \(f(x)\) in Effigy \(\PageIndex{xxx}\).
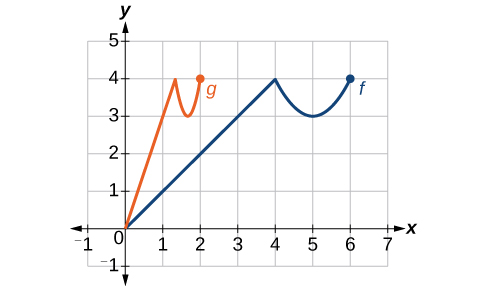
Solution
The graph of \(thousand(x)\) looks like the graph of \(f(x)\) horizontally compressed. Because \(f(10)\) ends at (6,iv) and \(grand(x)\) ends at (2,4), we can see that the x-values take been compressed by \(\frac{1}{3}\), considering \(half-dozen(\frac{1}{iii})=2\). We might besides find that \(yard(2)=f(vi)\) and \(g(i)=f(3)\). Either way, we can draw this relationship as \(k(10)=f(3x)\). This is a horizontal pinch by \(\frac{1}{3}\).
Assay
Notice that the coefficient needed for a horizontal stretch or pinch is the reciprocal of the stretch or pinch. And then to stretch the graph horizontally by a scale factor of four, we demand a coefficient of \(\frac{ane}{4}\) in our function: \(f(\frac{i}{4}x)\). This means that the input values must be 4 times larger to produce the aforementioned effect, requiring the input to be larger, causing the horizontal stretching.
Exercise \(\PageIndex{eleven}\)
Write a formula for the toolkit square root function horizontally stretched by a factor of 3.
- Respond
-
\(k(x)=f(\frac{ane}{three}ten)\), so using the square root office nosotros get \(m(x)=\sqrt{\frac{ane}{3}ten}\)
Performing a Sequence of Transformations
When combining transformations, it is very of import to consider the guild of the transformations. For example, vertically shifting by three and and then vertically stretching by ii does non create the aforementioned graph every bit vertically stretching by 2 and and then vertically shifting past 3, because when we shift offset, both the original office and the shift get stretched, while only the original function gets stretched when nosotros stretch beginning.
When we meet an expression such every bit \(2f(ten)+iii\), which transformation should we start with? The reply here follows nicely from the guild of operations. Given the output value of \(f(x)\), we first multiply past ii, causing the vertical stretch, then add 3, causing the vertical shift. In other words, multiplication before addition.
Horizontal transformations are a little trickier to think about. When we write \(one thousand(x)=f(2x+3)\), for example, we have to think about how the inputs to the function \(yard\) chronicle to the inputs to the function \(f\). Suppose nosotros know \(f(7)=12\). What input to \(g\) would produce that output? In other words, what value of \(ten\) will permit \(g(x)=f(2x+3)=12?\) We would need \(2x+3=7\). To solve for \(ten\), we would first subtract three, resulting in a horizontal shift, and then split up by 2, causing a horizontal pinch.
This format ends upward being very hard to work with, considering it is ordinarily much easier to horizontally stretch a graph earlier shifting. We tin piece of work effectually this by factoring within the function.
\[f(bx+p)=f(b(x+\frac{p}{b})) \nonumber\]
Let's piece of work through an example.
\[f(ten)=(2x+4)^2 \nonumber\]
We tin gene out a two.
\[f(ten)=(2(10+2))^2 \nonumber\]
Now nosotros can more clearly find a horizontal shift to the left 2 units and a horizontal compression. Factoring in this way allows us to horizontally stretch offset and so shift horizontally.
Combining Transformations
- When combining vertical transformations written in the form \(af(x)+k\), start vertically stretch by \(a\) and then vertically shift by \(thou\).
- When combining horizontal transformations written in the form \(f(bx+h)\), get-go horizontally shift by \(h\) and then horizontally stretch by \(\frac{one}{b}\).
- When combining horizontal transformations written in the course \(f(b(10+h))\), showtime horizontally stretch past \(\frac{1}{b}\) and then horizontally shift by \(h\).
- Horizontal and vertical transformations are independent. It does not matter whether horizontal or vertical transformations are performed starting time.
Case \(\PageIndex{20}\): Finding a Triple Transformation of a Tabular Part
Given Tabular array \(\PageIndex{18}\) for the function \(f(x)\), create a tabular array of values for the office \(g(x)=2f(3x)+1\).
| \(x\) | 6 | 12 | 18 | 24 |
|---|---|---|---|---|
| \(f(x)\) | 10 | 14 | 15 | 17 |
Solution
There are three steps to this transformation, and we volition work from the inside out. Starting with the horizontal transformations, \(f(3x)\) is a horizontal compression by \(\frac{1}{iii}\), which means nosotros multiply each \(x\)-value by \(\frac{ane}{3}\).Come across Table \(\PageIndex{nineteen}\).
| \(x\) | 2 | 4 | half dozen | 8 |
|---|---|---|---|---|
| \(f(3x)\) | x | 14 | xv | 17 |
Looking now to the vertical transformations, we kickoff with the vertical stretch, which will multiply the output values by two. We use this to the previous transformation. See Table \(\PageIndex{twenty}\).
| \(x\) | 2 | four | 6 | eight |
|---|---|---|---|---|
| \(2f(3x)\) | 20 | 28 | 30 | 34 |
Finally, we can apply the vertical shift, which will add together 1 to all the output values. See Table \(\PageIndex{21}\).
| \(ten\) | 2 | 4 | vi | viii |
|---|---|---|---|---|
| \(chiliad(x)=2f(3x)+ane+1\) | 21 | 29 | 31 | 35 |
Example \(\PageIndex{21}\): Finding a Triple Transformation of a Graph
Use the graph of \(f(x)\) in Effigy \(\PageIndex{31}\) to sketch a graph of \(k(x)=f\Big(\frac{1}{two}x+1\Big)−three\).
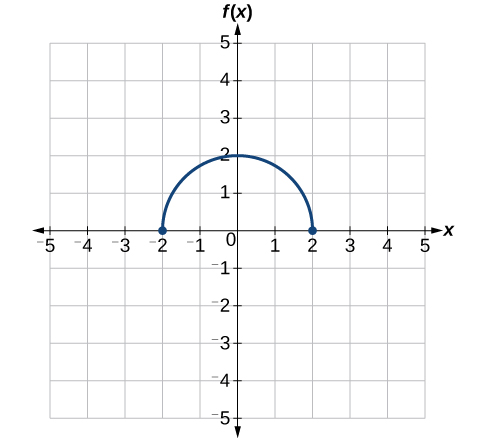
To simplify, let's starting time by factoring out the inside of the function.
\[f\Big(\dfrac{i}{2}x+1\Large)−3=f\Big(\dfrac{1}{ii}(x+2)\Large)−3\]
By factoring the inside, we can first horizontally stretch by two, every bit indicated by the \(\frac{1}{ii}\) on the inside of the function. Recollect that twice the size of 0 is still 0, and then the betoken \((0,2)\) remains at \((0,2)\) while the point \((2,0)\) will stretch to \((four,0)\). See Figure \(\PageIndex{32}\).
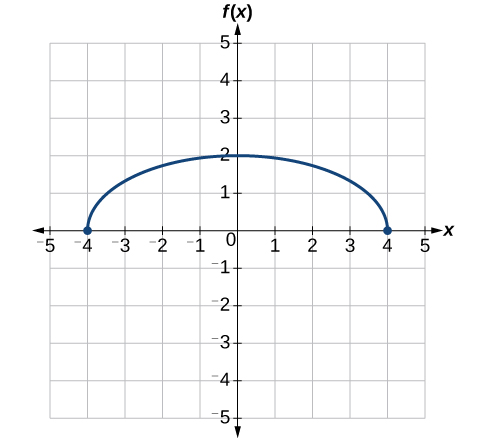
Next, we horizontally shift left by 2 units, as indicated by \(x+2\). See Figure \(\PageIndex{33}\).
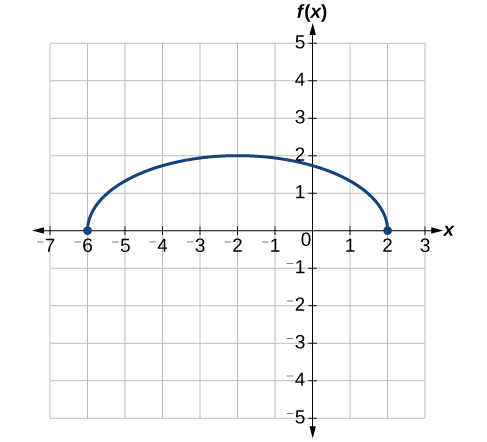
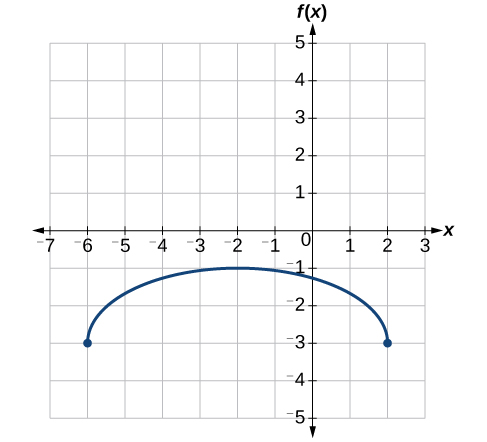
Last, nosotros vertically shift downward past 3 to complete our sketch, as indicated by the −3 on the exterior of the function. See Figure \(\PageIndex{34}\).
Fundamental Equations
- Vertical shift \(g(x)=f(x)+k\) (up for \(k>0\))
- Horizontal shift \(k(ten)=f(ten−h)\)(correct) for \(h>0\)
- Vertical reflection \(g(x)=−f(ten)\)
- Horizontal reflection \(g(x)=f(−x)\)
- Vertical stretch \(thou(x)=af(x)\) (a>0 )
- Vertical compression \(g(10)=af(x)\) (0<a<ane)
- Horizontal stretch \(g(x)=f(bx)(0<b<1)\)
- Horizontal compression \(1000(x)=f(bx)\) (b>1)
Key Concepts
- A role can be shifted vertically by calculation a constant to the output.
- A function can be shifted horizontally by calculation a constant to the input.
- Relating the shift to the context of a problem makes it possible to compare and interpret vertical and horizontal shifts.
- Vertical and horizontal shifts are ofttimes combined.
- A vertical reflection reflects a graph about the x-axis. A graph tin can be reflected vertically by multiplying the output by –i.
- A horizontal reflection reflects a graph near the y-centrality. A graph can be reflected horizontally by multiplying the input by –i.
- A graph tin can exist reflected both vertically and horizontally. The order in which the reflections are applied does not bear upon the final graph.
- A function presented in tabular course tin also be reflected by multiplying the values in the input and output rows or columns appropriately.
- A function presented as an equation tin be reflected by applying transformations one at a time.
- Even functions are symmetric almost the y-axis, whereas odd functions are symmetric most the origin.
- Even functions satisfy the condition \(f(x)=f(−10)\).
- Odd functions satisfy the status \(f(10)=−f(−ten)\).
- A role tin can exist odd, fifty-fifty, or neither.
- A part can be compressed or stretched vertically past multiplying the output past a constant.
- A role can be compressed or stretched horizontally by multiplying the input by a constant.
- The social club in which unlike transformations are applied does affect the concluding role. Both vertical and horizontal transformations must be applied in the order given. However, a vertical transformation may be combined with a horizontal transformation in whatsoever order.
Glossary
even function
a function whose graph is unchanged by horizontal reflection, \(f(ten)=f(−x)\), and is symmetric almost the y-axis
horizontal compression
a transformation that compresses a office's graph horizontally, past multiplying the input by a constant b>1
horizontal reflection
a transformation that reflects a function's graph across the y-centrality by multiplying the input by −ane
horizontal shift
a transformation that shifts a office's graph left or correct by adding a positive or negative constant to the input
horizontal stretch
a transformation that stretches a function'south graph horizontally past multiplying the input by a constant 0<b<ane
odd role
a function whose graph is unchanged by combined horizontal and vertical reflection, \(f(x)=−f(−x)\), and is symmetric about the origin
vertical compression
a function transformation that compresses the function'due south graph vertically by multiplying the output by a constant 0<a<1
vertical reflection
a transformation that reflects a part's graph beyond the x-axis past multiplying the output past −1
vertical shift
a transformation that shifts a role's graph upward or down by adding a positive or negative constant to the output
vertical stretch
a transformation that stretches a part'south graph vertically by multiplying the output past a constant a>1
Vertical Shift In An Equation,
Source: https://math.libretexts.org/Bookshelves/Algebra/Map:_College_Algebra_%28OpenStax%29/03:_Functions/3.06:_Transformation_of_Functions
Posted by: whitehavager.blogspot.com


0 Response to "Vertical Shift In An Equation"
Post a Comment