Which Quadrilateral Is A Kite

Proving that a quadrilateral is a kite is a piece of cake. Normally, all you accept to do is use congruent triangles or isosceles triangles. Here are the two methods:

If two disjoint pairs of consecutive sides of a quadrilateral are congruent, then it's a kite (reverse of the kite definition).
If one of the diagonals of a quadrilateral is the perpendicular bisector of the other, then it's a kite (converse of a property).

When you're trying to testify that a quadrilateral is a kite, the following tips may come in handy:

Bank check the diagram for coinciding triangles. Don't fail to spot triangles that look congruent and to consider how CPCTC (Corresponding Parts of Congruent Triangles are Coinciding) might help you.
Keep the first equidistance theorem in mind (which you might use in addition to or instead of proving triangles congruent): If two points are each (1 at a time) equidistant from the endpoints of a segment, and so those points make up one's mind the perpendicular bisector of the segment. (Here's an piece of cake way to think about it: If y'all have 2 pairs of coinciding segments, then at that place's a perpendicular bisector.)
Draw in diagonals. Ane of the methods for proving that a quadrilateral is a kite involves diagonals, and so if the diagram lacks either of the kite's two diagonals, endeavour drawing in one or both of them.

Now become gear up for a proof:

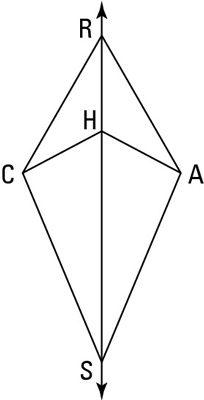
Game plan: Here'southward how your plan of attack might work for this proof.

Note that one of the kite's diagonals is missing. Draw in the missing diagonal, segment CA.
Check the diagram for congruent triangles. After cartoon in segment CA, at that place are half-dozen pairs of congruent triangles. The two triangles near likely to aid yous are triangles CRH and ARH.
Show the triangles congruent. You can use ASA (the Angle-Side-Angle theorem).
Use the equidistance theorem.

And so, using the equidistance theorem, those 2 pairs of congruent sides make up one's mind the perpendicular bisector of the diagonal you drew in. Over and out.

Check out the formal proof:

Statement 1 :

Reason for statement one : 2 points make up one's mind a line.

Statement 2 :

Reason for argument 2 : Given.

Statement 3 :

Reason for statement 3 : Definition of bisect.

Argument 4 :

Reason for statement 4 : Reflexive Holding.

Statement 5 :

Reason for argument five : Given.

Argument 6 :

Reason for statement half-dozen : Definition of bifurcate.

Statement vii :

Reason for statement 7 : If two angles are supplementary to two other congruent angles (angle CHS and angle AHS), then they're congruent.

Statement eight :

Reason for statement 8 : ASA (3, 4, 7).

Statement 9 :

Reason for statement nine : CPCTC.

Statement 10 :

Reason for statement x : CPCTC.

Statement 11 :

Reason for statement 11 : If ii points (R and H) are each equidistant from the endpoints of a segment (segment CA), then they make up one's mind the perpendicular bisector of that segment.

Statement 12 :

Reason for argument 12 : If one of the diagonals of a quadrilateral (segment RS) is the perpendicular bisector of the other (segment CA), then the quadrilateral is a kite.